【学习笔记】计算机科学概论

发表于 2023-07-20 更新于 2024-02-26 分类于笔记阅读次数：

这是《计算机科学概论（原书第13版）》的学习笔记，本文主要包括以下内容：

第一章数据存储

逻辑门
C 中的字符常量
二进制中的补码与余码
- 补码记数法
- 余码记数法

第十二章计算理论

可计算性
Bare Bones 语言
- 复制操作
- 交换操作
- 分支结构
停机问题
RSA

第一章数据存储

逻辑门

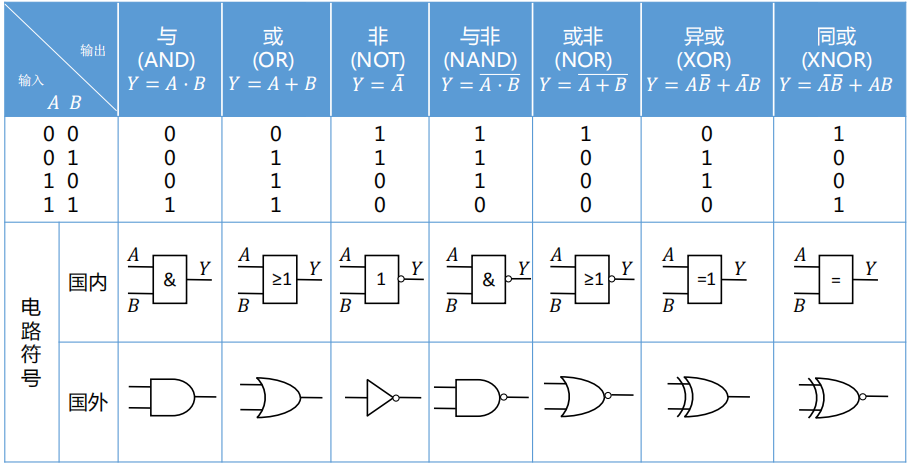
这八个基础的逻辑门的符号需要记清楚。记忆的技巧也很简单，N 就是右侧加一个小圆圈，X 就是左侧加一条线。“与”和“或”的符号我总是弄混淆，后来问了一下 skyhappy，他跟我讲：

我是这么记的，看输出端如果是与运算，就得有容乃大，所以开口得胖一点或运算就不需要了，所以窄一点就好了

我觉得很有道理。

~~于是联想到了一个经典Stack Overflow 笑话——在 C# 语言中如何实现“同或 (XNOR) ”操作~~

C 中的字符常量

在大一下学期学习《计算机程序设计基础》这门课的时候，老师上课说有同学将一个字符串定义成 char str = '123';，虽然 他通过了编译，但这是错误的。

关注的重点在于 他通过了编译，于是我上网查找了一下“单引号内如果包含多个字符为什么会编译成功”。

在 C/C++ 中，一个 int 类型占用的空间是 32 bit，即 4 个 byte。一个 char 类型占用的空间是 8 bit，即 1 个 byte。所以 ' 内一共可以最多包含 4 个字符，它会被看做成一个 int 类型的常量。其实就是四个 char 并排组在一起就成为了一个 int。

例如，('1' << 8) + '2' 和 '12' 是一模一样的，均为 (int)12594。

如果 ' 内字符大于或等于 2 个，编译器会警告：

1	warning: multi-character character constant [-Wmultichar]

如果大于或等于 5 个，编译器会警告：

1	warning: character constant too long for its type

二进制中的补码与余码

补码记数法

在补码记数法中，一个 有符号整数 用一个 32 bit 二进制串来表示，其中最左侧被称为“最高位”，最右侧被称为“最低位”。最高位表示 \(-2^{31}\)，其余各位分别表示 \(2^{30}, \cdots, 2^1, 2^0\)。因此一个 32 bit 二进制串的表示范围为 \([-2^{31}, 2^{31}-1]\)。

一个通过补码记数法记录的整数，通过“按位取反再加一”的方式可以得到自己的相反数。

余码记数法

在余码记数法中，“0”被定义为最高位为 1，其余位均为 0 的数。这个数在所有 32 bit 二进制串中恰好排在“差不多”中间的位置。比它大的数即为正数，比它小的数即为负数。

余码记数法和补码记数法的唯一区别是最高位的值相反。

第十二章计算理论

可计算性

一个函数，如果依据输入，通过算法，可以确定输出值，则它被称为 可计算的。事实上，存在那么一些函数，它们过于复杂以致找不到定义明确的、有限步骤的过程来根据输入确定输出。这样的函数计算超出了任何算法系统的能力范围，它们是 不可计算的。

一个函数是否可计算是非常重要的。如果确定了一个问题（以及数学建模后对应的函数）是不可计算的，那么人们就可以不必花更多精力研究如何用计算机来解决它，而是求助于其他更有效的方法。

Bare Bones 语言

一个通用程序设计语言。

一种基本数据类型。

所有的变量本质上都是二进制数。
三条赋值语句。

clear name 表示把 name 清零。 incr name 表示使 name 自增 1。 decr name 表示使 name 自减 1。
一条控制结构语句。

while name not 0: 在 name 不为 0 的时候，会一直做下方缩进的语句或语句序列（和 Python 类似）。

定理：Bare Bones 语言能够用来表达计算所有图灵可计算函数的算法。

复制操作、交换操作、分支结构等特性都可以使用 Bare Bones 语言实现。

复制操作

while x not 0:
  incr z
while z not 0:
  incr x
  incr y

这样就通过辅助变量 z 完成了 y = x 的复制操作。我们将其简写为 copy x to y。

交换操作

既然能够完成复制操作，那么也一定能够完成交换操作。

分支结构

我们现在想实现类似

if x:
  // ... do sth1
else:
  // ... do sth2

的结构。

copy x to z
clear w
incr w
while z not 0:
  // do sth1
  clear z
  decr w
while w not 0:
  // do sth 2

以上代码可以实现这样的 if-else 分支结构。

停机问题

如果程序中所有的变量都是用程序自身的编码表示（把字符全部转为二进制串）来进行初始化的，且这个程序在有限步骤后能够停止，则称这个 Bare Bones 程序是 自终止的。

停机问题指的是，是否存在一个算法，能够判断一个 Bare Bones 程序是否是自终止的。

答案是不存在。证明停机问题不可解，采取的方式是反证法。

假设有一个 Bare Bones 程序 A，它接受的输入是一段 Bare Bones 程序 test，产生的输出是 test 是否是自终止的：若是自终止的，则输出 1；若不是自终止的，则输出 0。

假设把 A 所得输出放入变量 x。考虑在 A 后添加

1
2
3

// A...
// x = output
while x not 0:

我们称这个新的程序为 B。接下来我们要证明 B 既不是自终止的，也不是非自终止的，以此推导出矛盾。

若 B 是自终止的：

将 B 作为自己的输入，则 x 为 1。此时进入 while 死循环，则 B 不是自终止的。矛盾。
若 B 是非自终止的：

将 B 作为自己的输入，则 x 为 0。此时不进入 while 循环，则 B 是自终止的。矛盾。

所以，如果停机问题可解，也就是说，存在一个程序 A，使得它能判断一段 Bare Bones 程序是否是自终止的，那么我们就可以构造出一个矛盾的程序 B。因此停机问题不可解。

RSA

RSA 是一种经典的公钥加密系统，被广泛应用于加密信息传递。~~尤其是树洞上的信息加密。~~

RSA 密钥的生成与分发

\(\lambda(n)\) 为 Carmichael function，是指最小的正整数 \(m\)，满足对于所有的与 \(n\) 互质的 \(a\)，均有 \(a^{m} \equiv 1 \pmod n\)。

选择两个大质数 \(p, q\)，记 \(n = pq\)。
计算 \(\lambda(n) = \mathrm{lcm}(p - 1, q - 1)\)。
选择一个 \(e\) 使得 \(e\) 与 \(\lambda(n)\) 互质。
计算 \(d\) 满足 \(d \equiv e^{-1} \pmod{\lambda(n)}\)。

\(n, e\) 作为公钥，\(d\) 作为密钥。

RSA 的加密与解密

由于所有的运算都会对 \(n\) 取模，所以一个很自然的要求是明文 \(m\) 的长度小于 \(n\)。

加密：密文 \(c \equiv m^e \pmod n\)
解密：明文 \(m \equiv m^{de} \equiv c^d \pmod n\)

RSA 的正确性

只需要证明 \(m \equiv m^{de} \pmod {pq}\) 即可，更简化地说，只需要证明 \(m \equiv m^{de} \pmod p\) 即可，对 \(q\) 同理。

由于 \(de \equiv 1 \pmod {\lambda(pq)}\)，而 \(\lambda(pq) = (p - 1)(q - 1)\)。所以不妨记 \(de - 1 = h(p - 1) = k(q - 1)\)。

若 \(m \equiv 0 \pmod p\)，则 \(m^{ed} \equiv 0 \equiv m \pmod p\)。
若 \(m \not\equiv 0 \pmod p\)，则由费马小定理 \(m^{p-1} \equiv 1 \pmod p\)。

\[ m^{de} \equiv m^{1 + h(p - 1)} \equiv m \cdot (m^{p-1})^h \equiv m \cdot 1^{h} \equiv m \pmod p \]

因此命题得证。

第一章 数据存储

逻辑门